Tree merupakan salah satu bentuk struktur data bukan linier yang menggambarkan bentuk hierarki antara elemen-elemen. Tree biasanya terdiri dari root (akar) dan node-node (simpul-simpul) yang berada di bawah root. Struktur seperti tree sangat banyak sekali dgunakan dalam dunia nyata, misalnya: struktur organisasi suatu perusahaan, pengaturan filesystem, daftar isi sebuah buku, dan masih banyak lagi.
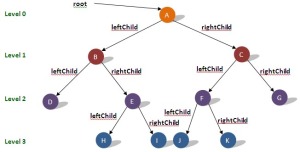
Ilustrasi struktur data tree:
Degree (derajat) adalah jumlah edge yang keluar dan masuk dari sebuah node.
Contoh : node E memiliki in degree 1 dan out degree 2
Root (akar) adalah node yang memiliki derajat keluar >=0 dan derajat masuk = 0.
Contoh : node A adalah root
Subtree / child adalah bagian salah satu node dibawah root sampai ke bawah.
Contoh : tree C adalah right subtree dari A dan tree B merupakan left subtree dari A
node G dan F merupakan child dari node C
node F merupakan parent dari node J dan K
Ancestor adalah Node yang berada di atas node lain.
Contoh : node B adalah ancestor dari node E
Descendant adalah node yang berada di bawah node lain.
Contoh : node E adalah descendant dari node A.
Leaf (daun) adalah semua node yang derajat masuknya 1 dan derajat keluarnya 0.
Contoh : node D, H, I, J, K, dan G adalah leaf
Sibling adalah node yang mempunyai level yang sama dan parent yang sama.
Contoh : node D adalah sibling dari node A
Height (ketinggian) adalah level tertinggi dari tree ditambah 1.
Contoh : height dari tree A adalah 3 + 1 = 4
Weight (bobot) adalah jumlah leaf(daun) pada tree.
Contoh : weight dari tree A adalah 6
BINARY TREE
Sebuah tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal 2 subtree yang disebut sebagai subpohon kiri(left subtree) dan subpohon kanan (right subtree) dan kedua subtree tersebut harus terpisah, atau dengan kata lain tiap node dalam binary tree hanya boleh memiliki paling banyak 2 child.
Binary tree terdiri dari :
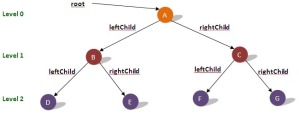
- Full Binary Tree : semua node (kecuali leaf pasti memiliki 2 anak dan tiap subtree memiliki panjang path yang sama)
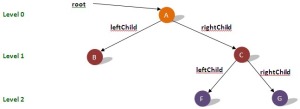
- Complete Binary Tree : mirip dengan full binary tree, tetapi tiap subtree boleh memiliki panjang path yang berbeda dan tiap node (kecuali leaf memiliki 2 anak)
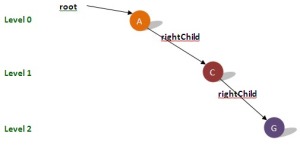
- Skewed Binary Tree : binary tree yang semua nodenya (kecuali leaf) hanya memiliki satu anak
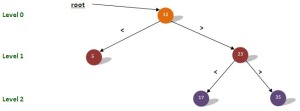
BINARY SEARCH TREE
Binary tree dengan sifat bahwa nilai dari semua left child harus lebih kecil daripada nilai dari right child dan parentnya.
Contoh :
Contoh Implementasi Binary Search Tree :
/**
* Program membuat binary tree yang memiliki 2 anak dimana insertion
* dilakukan secara terurut, dimana data yang lebih kecil diletakkan di kiri
* dan yang lebih besar diletakkan di kanan.
* @author : Jeffrey Hermanto Halimsetiawan
* Selasa, 1 April 2008
**/
import java.util.*;
class Node{
int data;
Node left;
Node right;
Node(int x){
this.data = x;
}
}
public class BinTree{
private Node root;
/**
* Mengecek apakah tree masih kosong
**/
private boolean isEmpty(){
return (root == null);
}
/**
* Memasukkan suatu nilai ke dalam tree.
* Jika nilai tersebut lebih kecil dari nilai node, maka bergerak ke kiri terus
* hingga menjadi child, begitu juga sebaliknya.
**/
public void insert(int input){
Node temp = new Node(input);
if (isEmpty())
root = temp;
else {
Node cursor = root,
parent = null;
while (cursor != null){
parent = cursor;
if (input < cursor.data)
cursor = cursor.left;
else
cursor = cursor.right;
}
/**
* Menambahkan Node baru pada kiri/kanan Node parent bergantung
* pada nilai input dan nilai yang disimpan Node parent
**/
if (input < parent.data){
parent.left = temp;
return;
}
else {
parent.right = temp;
return;
}
}
}
/**
* Mencari suatu nilai dalam tree berdasarkan prinsip :
* Selama belum menemukan nilai yang sama,
* Jika nilai yang dicari lebih kecil dari nilai yang disimpan dalam Node
* maka bergerak ke left Child begitu juga sebaliknya.
**/
public Node find(int key){
Node cursor = root;
while (cursor != null){
if (cursor.data == key)
return cursor;
else if (key < cursor.data)
cursor = cursor.left;
else
cursor = cursor.right;
}
return null;
}
public boolean delete(int key){
Node cursor = root,
parent = null;
boolean found = false,
isLeftChild = true; //menandai apakah Node yang dihapus merupakan left child
if (!isEmpty()){
while (cursor != null){
parent = cursor;
if (key == cursor.data){
found = true;
break;
}
else if (key < cursor.data){
isLeftChild = true;
cursor = cursor.left;
}
else {
isLeftChild = false;
cursor = cursor.right;
}
}
if (!found)
return false;
else {
/**
* Untuk menghapus leaf (tidak punya child)
**/
if (cursor.left == null && cursor.right == null){
if (cursor == root)
root = null;
else if (isLeftChild)
parent.left = null;
else
parent.right = null;
}
/**
* Jika node yang akan dihapus hanya memiliki salah satu subtree
* maka tinggal memindahkan subtree menggantikan node yang dihapus
**/
else if (cursor.left == null){
if (cursor == root)
root = cursor.right;
else if (isLeftChild)
parent.left = cursor.right;
else
parent.right = cursor.right;
}
else if (cursor.right == null){
if (cursor == root)
root = cursor.left;
else if (isLeftChild)
parent.left = cursor.left;
else
parent.right = cursor.left;
}
/**
* Jika node yang akan dihapus memiliki 2 child, maka cari successornya
* dengan fungsi getSuccessor kemudian hubungkan subtree bagian kanan
* dari node yang dihapus dengan successor
**/
else {
Node successor = getSuccessor(cursor);
if (cursor == root)
root = successor;
else if (isLeftChild)
parent.left = successor;
else
parent.right = successor;
//menyambung successor dengan cursor.right
successor.right = cursor.right;
}
}
}
return true;
}
/**
* Mencari nilai terbesar yang mendekati nilai yang disimpan Node
* yang dihapus, Ilustrasi :
*
* 65
* 59 72
* 32 64
* 62
* misal : nilai yang dihapus 65, maka nilai terbesar yang mendekati adalah 64.
* maka ambil 64 sebagai successor, kemudian gabungkan
* 59
* 32 63
* Kemudian satukan keduanya :
* 64
* 59
* 32 63
* Jadilah urutan tree yang masih memenuhi syarat Binary Search Tree
**/
private Node getSuccessor(Node localNode){
Node parent = null,
successor = localNode,
cursor = localNode.left;
while (cursor != null){
parent = successor;
successor = cursor;
cursor = cursor.right;
}
if (successor != localNode.left){
parent.right = successor.left;
successor.left = localNode.left;
}
return successor;
}
/**
* Method traverse untuk mengelilingi Node-Node dalam tree
**/
public void traverse(int tipe){
switch (tipe){
case 1:
System.out.print("\nPreorder traversal:\n");
preOrder(root);
break;
case 2:
System.out.print("\nInorder traversal:\n");
inOrder(root);
break;
case 3:
System.out.print("\nPostorder traversal:\n");
postOrder(root);
break;
}
System.out.println('\n');
}
private void preOrder(Node localRoot){
if (localRoot == null) return;
System.out.print(localRoot.data+" ");
preOrder(localRoot.left);
preOrder(localRoot.right);
}
private void inOrder(Node localRoot){
if (localRoot == null) return;
inOrder(localRoot.left);
System.out.print(localRoot.data+" ");
inOrder(localRoot.right);
}
private void postOrder(Node localRoot){
if (localRoot == null) return;
postOrder(localRoot.left);
postOrder(localRoot.right);
System.out.print(localRoot.data+" ");
}
}
No comments:
Post a Comment